The Binary Options: What are and how they work

The Binary Options are a financial instrument and a type of Option; these options are called “Binary” because they have only two possible outcomes, one that is positive and one that is negative. The Binary Options ask to the Traders to make a prediction about the movement of the Prices of a Asset (Asset that you can choose), and in case that this prediction is correct after a certain period of time (Called expiry time), the Traders will take a profit (The Payout) whereas in case that the prediction is wrong, the Traders will lose the money invested on the Binary Option (Or a part of them).

There are a lot of different Assets on which is possible to do these “predictions”: from the most “famous” and “listed” stocks (As Apple, Google, Coca-Cola, IBM, Ebay, Twitter, Facebook, McDonald’s, Goldman Sachs, Barclays, etc… ) to the pair of currency (As EUR/USD, GBP/EUR, GBP/USD, etc… ) and from the commodities (As Gold, Silver, Corn, Crude Oil, Sugar, etc… ) to the most famous stock market indices (As NASDAQ, S&P500, DOW, DAX, FTSE100, etc… ).
As you can see, there are hundreds of different Asset (That vary from Broket to Broker) and for this reason the Traders have freedom of choice.

For example:
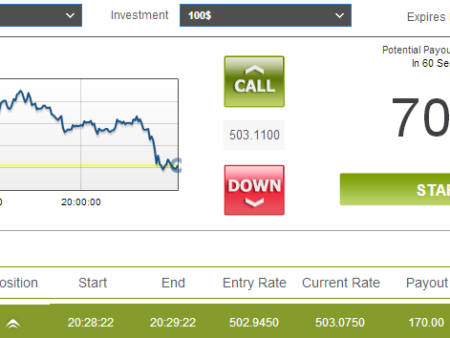
There is a Binary Option on a certain Asset, for example Apple, and the Binary Option requires us to predict if the Price (Of the Asset, in this case the shares of Apple), once it’s reached the Expiry time, will be higher or lower (than the current Price). Let’s say that the value of the shares of Apple is of $85,50 and that we predict that there will be a rise in Prices: after we will choose the correct Binary Option for our prediction, we have to wait the end of the Expiry Time. Let’ say that the expiry time in this case was of 15 minutes; after 15 minutes, we will know if our prediction was correct or wrong. If the Price of the shares after 15 minutes is of $86,20 (Or at least of $85,51), our prediction was correct and for this reason we will have the Payout; whereas if the Price of the Shares after 15 minutes is of $83,80 (Or at least of $85,49), our prediction was wrong and for this reason we will lose the money that we have invested on the Binary Option (Or a part of them).

This was an example of a type of Binary Options, called High/Low or Up/Down, that is the standard one (But there are also other types of Binary Options). However, regardless of the type of Binary Option, they always “ask” to us to make a prediction, and to choose one of the two possible outcomes (Regardless of the possible outcomes). As you have seen, the Binary Options are easy to understand and are nothing of complex (They are often considered as Betting, although they are not Betting), and this semplicity is the “strong point” of this financial instrument. But beware: operating in a correct way with the Binary Options it’s not so easy as it may seem.